
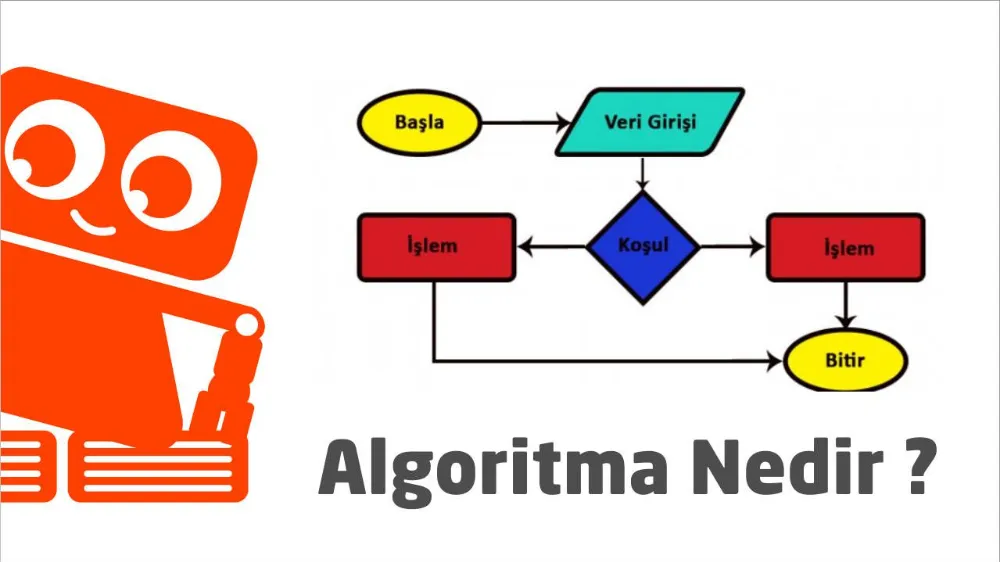
Bu terim, Ortaçağ Arap matematikçisi Al Khwarizmi'nin adından türetilmiştir. Algoritma kavramı, bilgisayar bilimleri, matematik, mühendislik ve diğer alanlarda çok önemlidir.
Algoritmanın kökeni, eski Yunan matematikçi Euclid'in, Öklidyen Algoritması adlı çalışmasıyla ilişkilidir. 300-200 M.Ö. yılları arasında yaşayan Euclid, en eski ve en etkili algoritmaları geliştiren matematikçilerden biridir. Onun çalışmaları, algoritmaların temelini oluşturan ve günümüzde bile kullanılan algoritma tanımının temelini atmıştır.
Algoritmaların kökeni ve tanımı, geçmişten günümüze birçok matematikçi, bilim insanı ve mühendis tarafından farklı şekillerde ele alınmıştır. Ancak her durumda, algoritmaların temel prensipleri, problem çözmek ve görevleri gerçekleştirmek adına adımların tanımlanması üzerine kuruludur.
Algoritmanın temel bileşenleri ve geliştirme süreçleri, bu temel tanımın detaylarına işaret eder. Ancak algoritmanın kökenine bakıldığında, onun temeldeki amacının problemleri ne kadar etkin bir şekilde çözmeye yardımcı olmak olduğu görülecektir.
Algoritmanın Temel Bileşenleri
Algoritma, bir problemi çözmek veya belirli bir görevi yerine getirmek için adım adım yönergelerin tanımlanmış bir setidir. Temel bileşenleri, giriş, çıkış, kontrol yapıları ve döngülerdir. Giriş, problemin veya görevin tanımı ve gereksinimleriyle ilgili verileri temsil eder. Çıkış, algoritmanın sonucudur ve genellikle girişe dayanır. Kontrol yapıları, algoritmanın akışını yönlendiren ifadelerdir. Döngüler ise belirli bir koşul gerçekleşene kadar belirli bir işlemi tekrarlamak için kullanılır.
Giriş, algoritmada işlenmesi gereken verilerin temsil edildiği kısımdır. Bu veriler, giriş parametreleri veya kullanıcının sağladığı veriler olabilir. Bu bileşen, sorunun tanımını ve gerçekleştirilmesi gereken görevi içeren veri setlerini içerir.
Çıkış, algoritmanın sonucunu temsil eder. Algoritmanın çalıştırılmasının ardından, işlenen giriş verilerine dayanılarak elde edilen sonuç, çıkış bileşeni olarak adlandırılır. Genellikle hangi tür verilerin algoritma tarafından oluşturulduğunu ya da dönüştürüldüğünü ifade eder.
Kontrol yapıları ve döngüler, algoritmanın akışını kontrol eden ifadelerdir. Kontrol yapıları, belirli koşullara dayalı olarak hangi adımların izleneceğini belirler. Döngüler ise belirli bir durum gerçekleşene kadar belirli bir işlemi tekrarlamak için kullanılır. Bu bileşenler, algoritmanın belirli koşullara bağlı olarak nasıl davranması gerektiğini belirler.
Algoritma geliştirme süreçleri, bir problemi çözmek veya bir görevi yerine getirmek için bir algoritmanın oluşturulması ve optimize edilmesi aşamalarını içerir. Bu süreç, problem analizi, algoritma tasarımı, kod geliştirme ve test etme aşamalarından oluşur.
Öncelikle, belirli bir problemi çözmek için ne tür bir algoritmanın gereklilik olduğunun belirlenmesi gerekir. Bu aşama, problem analizi olarak adlandırılır. Problem analizini tamamladıktan sonra, algoritma tasarımına geçilir. Bu aşamada, problemi çözmek için kullanılacak algoritmanın mantığı ve adımları belirlenir. Bu adımlar, genellikle akış diyagramları ve benzeri görsel araçlar kullanılarak gösterilir.
Algoritma tasarımı tamamlandıktan sonra, kod geliştirme sürecine geçilir. Burada, tasarlanan algoritma bir programlama dilinde yazılır ve hata ayıklama işlemleri yapılır. Son olarak, geliştirilen algoritma test edilir ve gerektiğinde optimize edilir. Bu süreç, algoritmanın doğruluğunu, performansını ve verimliliğini artırmak için gereklidir.
Algoritma geliştirme süreçleri, problem çözme becerilerinin geliştirilmesi ve bilgisayar bilimleri alanındaki temel kavramların anlaşılmasını sağlar. Bu süreçler, genellikle teorik bilgiyi pratik uygulamalarla birleştirerek öğrenmeyi kolaylaştırır ve öğrencilere algoritmik düşünme becerileri kazandırır.
Algoritma Uygulama Sonuçları
Algoritma Uygulama Sonuçları, bir algoritmanın gerçek yaşamda nasıl performans sergilediğini ve beklenen sonuçları verip vermediğini değerlendirmeyi içerir. Algoritma geliştirme sürecinde yapılan testler sonucunda elde edilen veriler, algoritmanın verimli çalışıp çalışmadığını anlamak için kullanılır. Bu uygulama sonuçları, algoritmanın performansını değerlendirmek ve gerektiğinde düzeltmeler yapmak için önemlidir.
Algoritma uygulama sonuçları, genellikle test verileriyle elde edilir. Bu veriler, algoritmanın doğruluğunu, hızını, bellek kullanımını ve diğer performans ölçütlerini belirlemek için kullanılır. Algoritma uygulama sonuçları, algoritmanın işlevselliğini, güvenilirliğini ve kullanılabilirliğini değerlendirmek için kritik bir rol oynar.
Algoritma uygulama sonuçları ayrıca, geliştirme aşamasında yapılan düzeltmelerin etkinliğini değerlendirmek için de kullanılır. Bu sonuçlar, algoritmanın performansını iyileştirmek için hangi alanlarda çalışma yapılması gerektiğini belirlemeye yardımcı olur.
Algoritma uygulama sonuçları, algoritma geliştirme sürecinin en önemli aşamalarından biri olduğu için, titizlikle incelenmeli ve analiz edilmelidir. Bu sonuçlar, algoritmanın gerçek dünya problemlerini nasıl çözdüğünü ve kullanıcı ihtiyaçlarına nasıl cevap verdiğini ortaya koyar.